Search

Language Proficiency Enhanced Knowledge Tracing

Updated
2023/06/07 09:08
Keywords
Knowledge Tracing
Student Modeling
Learning Analytics
Language Proficiency
By
정희석 (AI Researcher) / poco2889@classting.com
3 more properties
Abstract. With an increasing interest in personalized learning, active research is being conducted on knowledge tracing to predict the learner’s knowledge state. Recently, studies have attempted to improve the performance of the knowledge tracing model by incorporating various types of side information. We propose a knowledge tracing method that utilizes the learner’s language proficiency as side information. Language proficiency is a key component of comprehending a question’s text and is known to be closely related to students’ academic performance. In this study, language proficiency was defined with Elo rating score and time window features, and was used in the knowledge tracing task. The dataset used in this study contains 54,470 students and 7,619,040 interactions, which were collected from a real-world online-learning platform. We conducted a correlation analysis to determine whether the language proficiency information of students was related to their ability to solve math word problems. In addition, we examined the effect of incorporating the language proficiency information on the knowledge tracing models using various baseline models. The analysis revealed a high correlation between the length of word problems and students’ language proficiency. Furthermore, in experiments with various baseline models, utilizing the language proficiency information improved the knowledge tracing model’s performance. Finally, when language proficiency information was incorporated, the cold start problem of the knowledge tracing model was mitigated. The findings of this study can be used as a supplement for educational instruction.

Introduction

As interest in personalized online learning grows, the research in the field of knowledge tracing (KT) to model a learner’s knowledge state also increases. Many studies have recently been conducted to improve the performance of the KT model by using various side information, such as response time [31,33], the number of attempts [10,43], question text [21,36], and relationship between concepts [9,23].
On the other hand, previous studies have found that the academic achievement in one subject is closely related to achievement in other subjects. For example, math grades are significantly correlated with science grades [16,39], while English grades have a significant impact on math and science grades [3,4]. As a result, if learning data from multiple subjects in which students participated can be collected, problem-solving information from one subject can be used to predict achievement in other subjects.
In particular, if we collect problem-solving performance data for students’ first language subjects (e.g., Korean, English, French, etc.), we can estimate their language proficiency (LP) information. LP is an important factor when learners acquire domain knowledge, and it has been shown to have a significant impact on academic performance in a variety of subjects [6,15,30,35]. Moreover, LP is an important factor in the learner’s problem solving. This is owing to the fact that learners must be able to read and comprehend the problem to complete it correctly [6]. For example, in mathematics, students with low LP are known to struggle with long word problems [37]. Therefore, LP information extracted from students’ problem-solving data of language subjects is likely to be useful for the KT task to predict their future performance in other subjects.
However, despite the fact that LP is an important factor in predicting students’ academic performance, to our knowledge, no study in the KT field has used this information. In addition, studies that used academic achievement data in one subject to predict the student’s knowledge state in another subject have not been sufficiently conducted.
In this study, we propose a KT method using LP information extracted from Korean problem solving data from students. First, we analyzed whether LP information was related to students’ math word problem performance. In addition, through experiments with real-world datasets, we predicted the knowledge state using students’ LP information and investigated whether using this information was effective in improving the performance of the KT model. Furthermore, we investigated whether using LP information can help mitigate the cold start problem.
As a result, the following research questions (RQs) were posed in this study, in an attempt to find answers.
RQ1 : Is there a correlation between students’ LP and their word problem performance?
RQ2 : Is it possible to improve the performance of the KT models by incorporating LP information?
RQ3 : Does utilizing LP information alleviate the cold start issue of the KT model?
The remainder of this paper is organized as follows. In Section 2, related works on deep learning-based knowledge tracing, students’ LP and academic performance, and the Elo rating system are presented. Section 3 describes the methodology used in the study. Sections 4 and 5 present the results and a discussion, respectively. Finally, Section 6 presents the conclusion of this study.

Related Works

Deep Learning-based KT

KT aims to estimate a learner’s knowledge state and predict future performance based on past learning histories. Typically, the learning history is represented by X=(e1,a1),(e2,a2),...,(et,at)X={(e_1,a_1),(e_2,a_2),...,(e_t,a_t)}. Here, ete_t denotes the exercise solved at time tt, and ata_t denotes the correctness of ete_t. As online education has grown in popularity, it has become possible to collect large amounts of learning activity data, and consequently, deep learning (DL)-based KT models are performing well. DL-based KT models include Recurrent Neural Network (RNN)-based models [29], Memory Augmented Neural Network (MANN)-based models [1,17,42], Attention Mechanism-based models [13,19,27,33], and Graph Neural Network (GNN)-based models [26,34,41]. Various studies have attempted to estimate the knowledge state more precisely by utilizing side information in addition to exercise and response data. According to [24], the side information used in the KT models can be categorized as question side information, student side information, and knowledge component (KC) side information. Question side information includes question text content [21,36] and question difficulty level [13,23,43], and so on. Student side information includes the number of attempts [10,43] and students’ prior knowledge [32], and so forth. As KC side information, relations between KCs, or questions [23] are used. In this study, the LP—which is student side information was used for the KT task.

Students’ LP and academic performance

When we learn something, we obtain a significant amount of information from text. Therefore, the LP is known to have a strong relationship with students’ academic performance. In other words, students with low LP inevitably learn little from the text [6]. Previous studies have found that LP influences academic performance in various subjects, including mathematics, science, and social sciences [6,15,30,35]. Especially in the case of mathematics, the ability to solve word problems is highly related to LP [37]. Word-problem solving differs from other types of mathematical competence; students are required to interpret text that explains a problem situation and deduce the number of sentences that represent that situation [12]. In particular, if LP is insufficient, calculation problems can be solved using key concept understanding, but not word problems. Consequently, there is a possibility that LP plays an important role in modeling a learner’s knowledge state. Therefore, in this study, LP was used as side information in the KT task to validate its effect.

Elo rating system

The Elo Rating System (ERS) [11] was used to estimate the relative ability of a chess player. ERS is a dynamic paired comparison model that is mathematically closely related to the one parameter logistic (1PL) IRT model [7]. Players are given a provisional ability score θθ at first, which is incrementally updated according to the weighted difference in match outcome S and the expected match outcome E(S)E(S) (Eq. 1). Here, K is a constant specifying the sensitivity of the estimate in the last attempt. The expected match outcome E(S)E(S) is calculated based on the difference between the ability estimates of both players j and k preceding the match, and expresses the probability of winning as in Eq. 2.
θj^=θj+K(Sj−E(Sj)),θ^k=K(Sk−E(Sk))\hat{\theta_{j}} = \theta_{j}+K(S_{j}-E(S_{j})), \hat{\theta}_{k}=K(S_{k}-E(S_{k}))
E(Sj)=11+10(θk−θj)400,E(Sk)=11+10(θj−θk)400\displaystyle \bold{E}(S_{j})={1 \over 1+10^{(\theta_{k}-\theta_{j}) \over 400}}, \bold{E}(S_{k})={1 \over 1+10^{(\theta_{j}-\theta_{k}) \over 400}}
If we interpret a student’s answer to a question as a match between the student and question, the ERS can be used to estimate learners’ proficiency and question difficulty. As the rating score is updated by a heuristic rule, this is simple, robust, and effective for adaptive educational systems [28].

Methodology

Language proficiency-enhanced knowledge tracing

The Elo rating score, calculated from the Korean problem-solving data, was used to estimate the students’ LP. A time window feature was used to reflect the time at which the Elo rating score was updated, based on the method of Lindsey et al. [20]. The reason for considering the timing information of the Elo rating score update is that students’ LP may change over time [5]. Because the students’ LP in this study was measured using data from Korean problem solving, if the student had not recently participated in Korean problem solving, the student’s Elo rating score would be fixed for a while. Therefore, by including a time window feature that contains information on the student’s Korean problem-solving by period, the possibility of a change in the student’s LP can be considered. The time window included information on the number of times the student attempted Korean problems and the number of correct answers by month, week, day, and hour. In addition, sentence length information from mathematical problems was used. Problem length was defined as the word count of each problem. 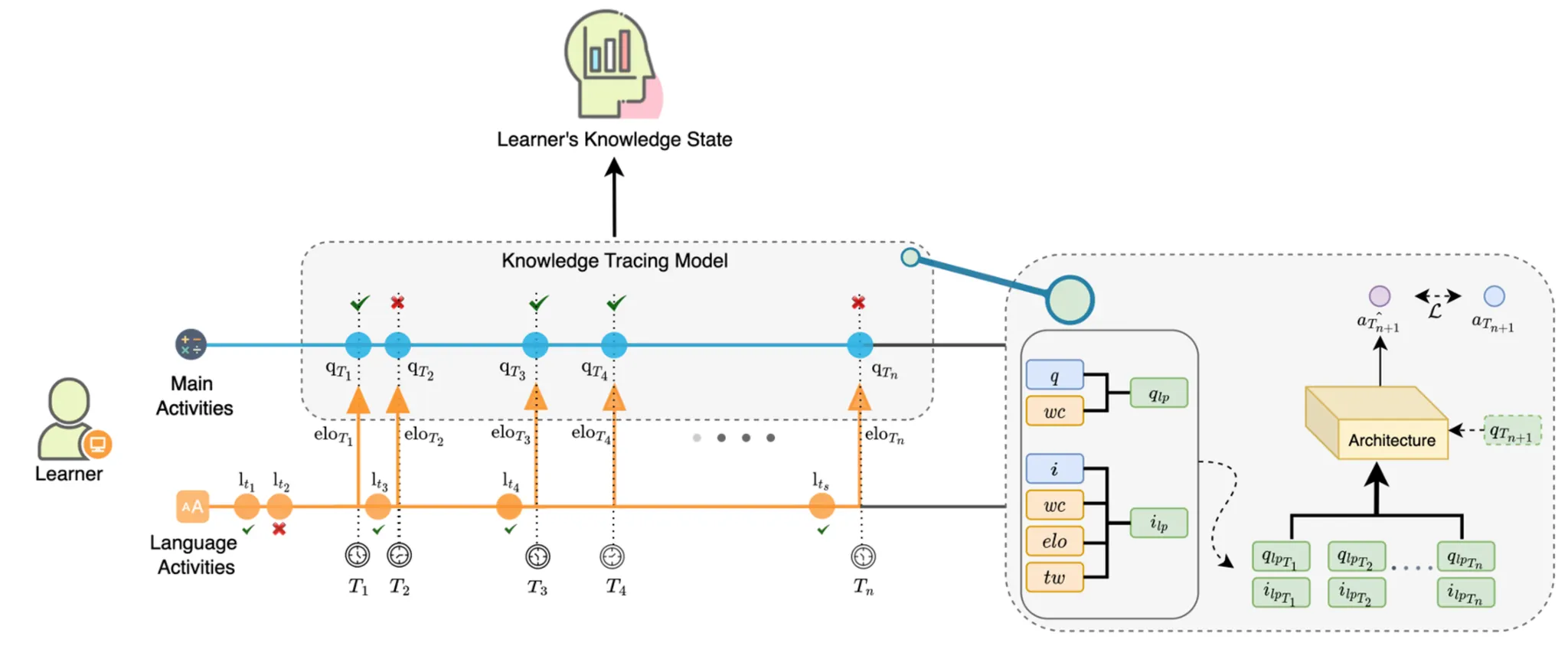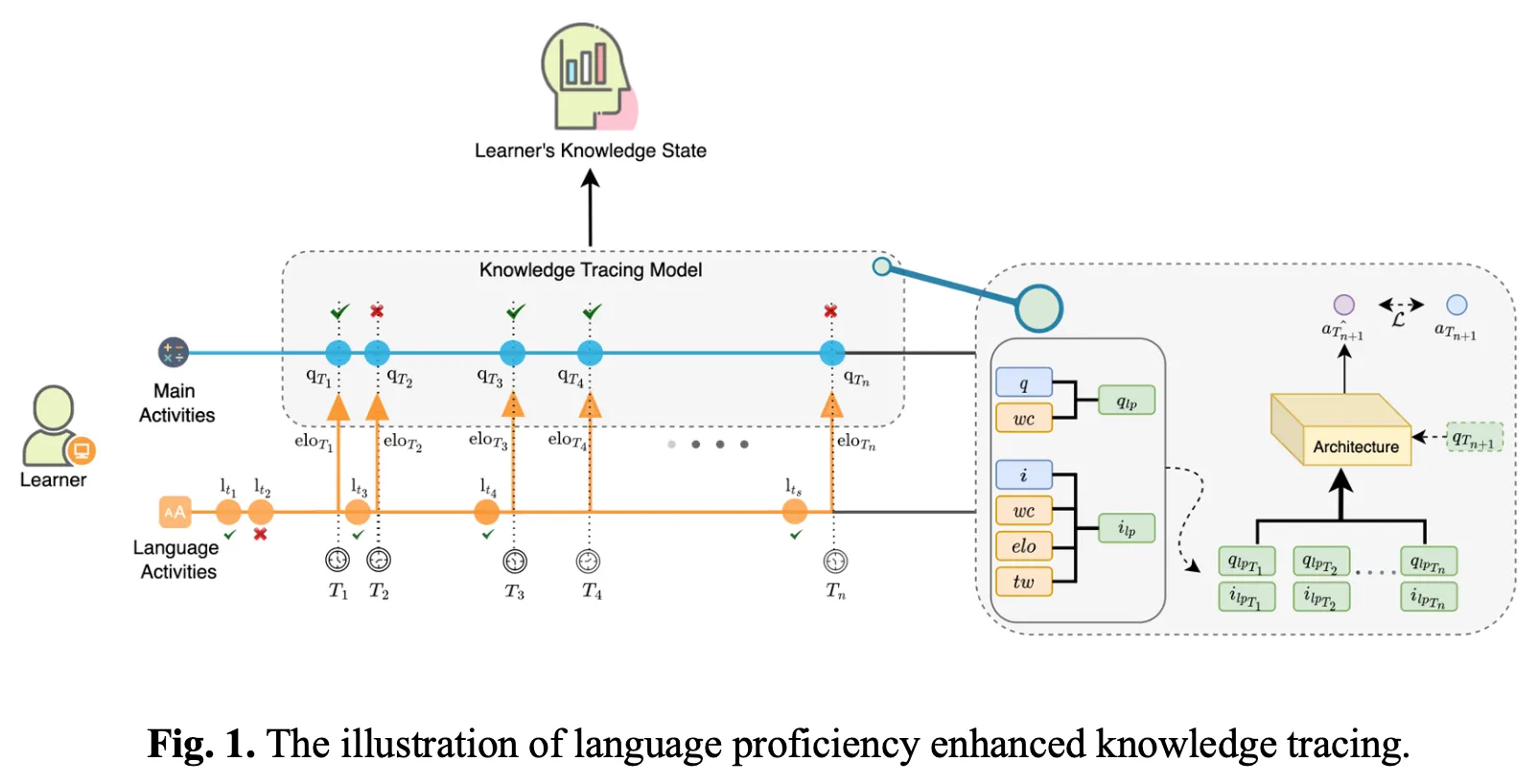Fig.1 shows the structure of the LP-enhanced KT model proposed in this study. qT1,qT2,⋯,qTnq_{T_1},q_{T_2},⋯,q_{T_n} indicate the questions of main activities, the math problem-solving event, whereas lt1,lt2,⋯,lts l_{t_1},l_{t_2},⋯,l_{t_s} indicate the questions of language activities, which is the Korean problem-solving event. T1,T2,⋯,TnT_1,T_2,⋯,T_n represent the timestamps of the main activities and t1,t2,⋯,tst_1,t_2,⋯,t_s represent the timestamps of the language activities. The Elo rating score calculated from the results of language activities up to TnT_n is used for timestamp TnT_n.
Compatibility with existing models was considered when incorporating the LP information into the model. Because most KT models utilize question embedding and/or interaction embedding, LP information was incorporated into the model as in Eq. 3.
qlp=W1T[q∥wc],  ilp=W2T[i∥wc∥elo∥tw]q_{lp}=W_1^T [q∥wc],\ \ i_{lp}=W_2^T [i∥wc∥elo∥tw]
Here, q refers to the question embedding. The interaction embedding of a tuple (q,aq,a), where q denotes the question and aa denotes the response (or correctness), is denoted by ii. ∥∥ denotes the concatenation. Elo rating score, word count, and each features in time window are continuous values. Like [33], we used trainable matrices for each LP related features and get embedding vectors eloelo,wcwc,twtw. The trainable parameters W1W_1 and W2W_2 project the concatenated vector to the size of the original question and interaction embedding, respectively. Final prediction and loss function are as follows:
aTn+1^=σ(Architecture(qlpT1:n,ilpT1:n))a_{\hat{T_{n+1}}} = \sigma(Architecture(q_{lp_{T_{1:n}}},i_{lp_{T_{1:n}}}))
L=BCE(aT^n+1,aTn+1)\mathcal{L} = BCE(a_{\hat{T}_n+1},a_{T_{n+1}})

Dataset

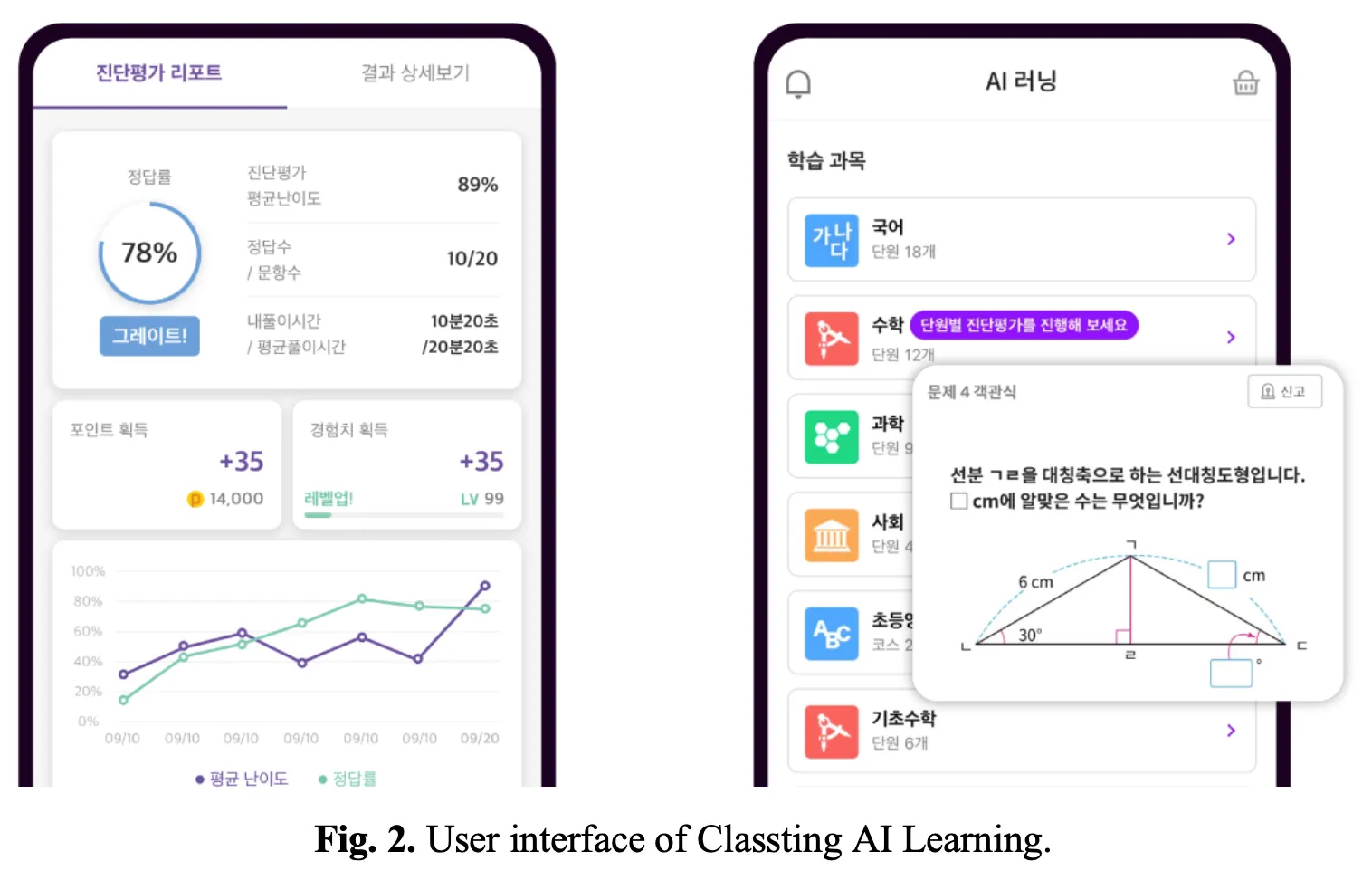
Data from Classting AI Learning1 were used in this study. Classting AI Learning is an online learning platform for K-12 that provides contents in Korean, English, mathematics, social studies, and science. Classting AI Learning currently has approximately three million users and is accessible via the web, Android, and iOS applications. Fig.2 shows the user interface of Classting AI Learning.
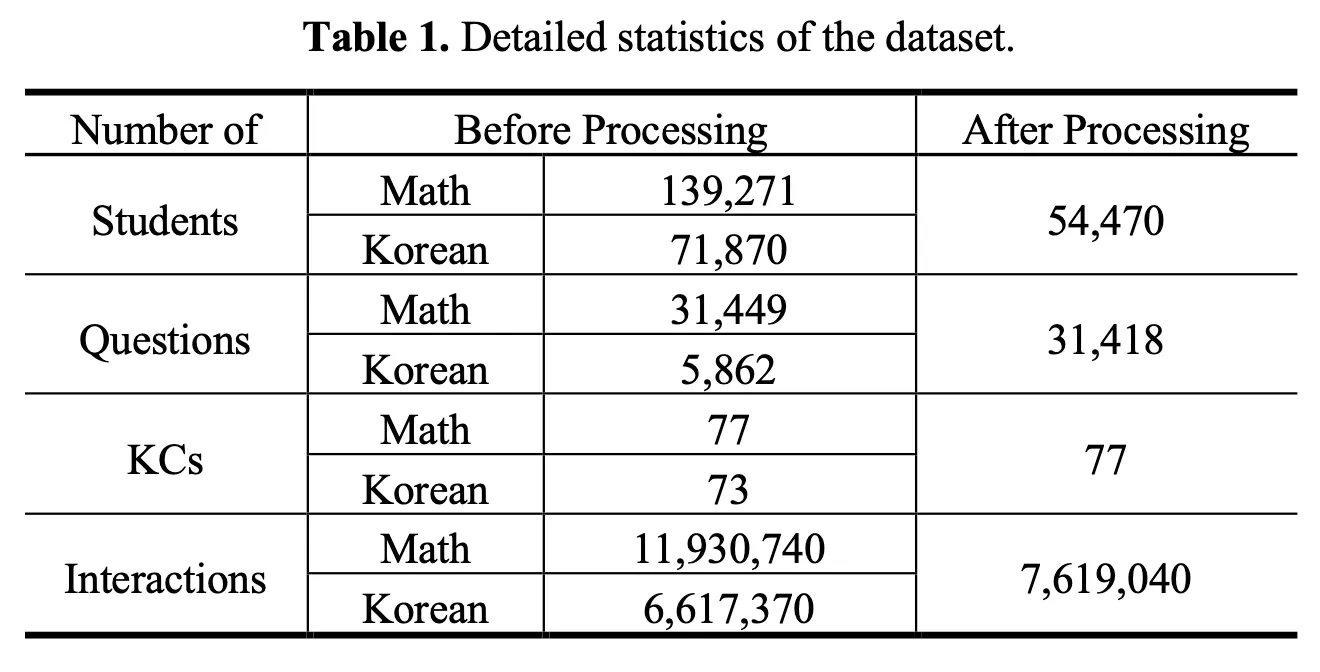
In this study, data collected in 2021 on students’ Korean and math problem-solving histories were used. First, LP information of students was extracted using Korean problem-solving data. The Korean problem-solving data included 71,870 students, 5,862 questions, 73 KCs, and 6,617,370 interactions. Using the learner’s LP information, we attempted to trace the learner’s knowledge in other subjects (math in this study). A total of 139,271 students, 31,449 questions, 77 KCs, and 11,930,740 interactions were included in the math problem-solving data. The data of students who solved less than five Korean and math problems were removed. As a result, data of 54,470 students, 31,418 questions, 77 KCs, and 7,619,040 interactions were used. Table 1 lists the detailed statistics of the dataset.

Baseline KT models

In this study, the following baselines were used to verify the effectiveness of the proposed LP-enhanced KT model:
•
DKT [29]: a representative RNN-based KT model that employs a single layer of LSTM [14] to estimate the learners’ knowledge state [8]
•
DKVMN [42]: a MANN-based model utilizing a static key memory to store latent KCs and a dynamic value memory to trace the mastery of corresponding KCs [22]
•
SAKT [27]: the first KT model to incorporate an attention mechanism [2]

Experimental Settings

A 5-fold cross validation was performed in which folds are split based on learners, whereby 10% of training set was used as the validation set. The performance was measured using 100 recent sequences of each learner [19]. Each model’s embedding size was set to 64; the learning rate was set to 0.001; the batch size was set to 256; and Adam optimizer [18] was used. The early stopping technique was used with 10-epoch patience according to validation AUC.

Correlation of LP and word problem performance

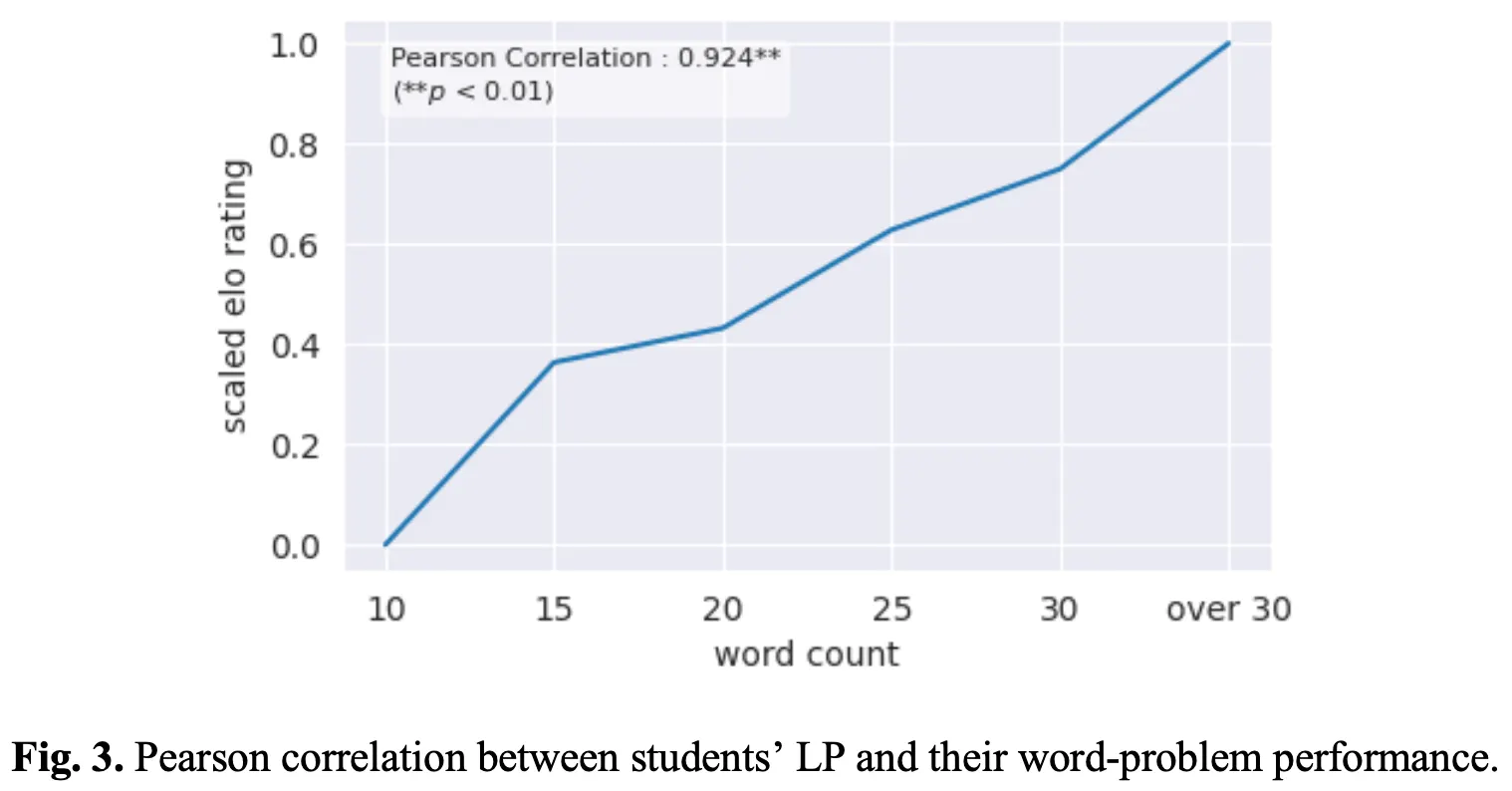
The Pearson correlation between the length of the math problem and the average Korean Elo rating score was examined for students who correctly responded to the problems to investigate the relationship between LP and math problem-solving performance. The length of a mathematical problem is defined as the number of words in a sentence. Pearson correlations were examined using Python SciPy 1.10.0 [38].

Results

Result of the correlation analysis between students’ LP and their word-problem performance (RQ1)

Fig.3 depicts the Pearson correlation analysis results between the length of the mathematical word problem and the average score of the Korean Elo rating score of students who correctly answered the problem. The length of the word problem sentences correlated strongly with the Korean Elo rating scores (Pearson Correlation = 0.924, p < 0.01).

Experimental results on KT models (RQ2)

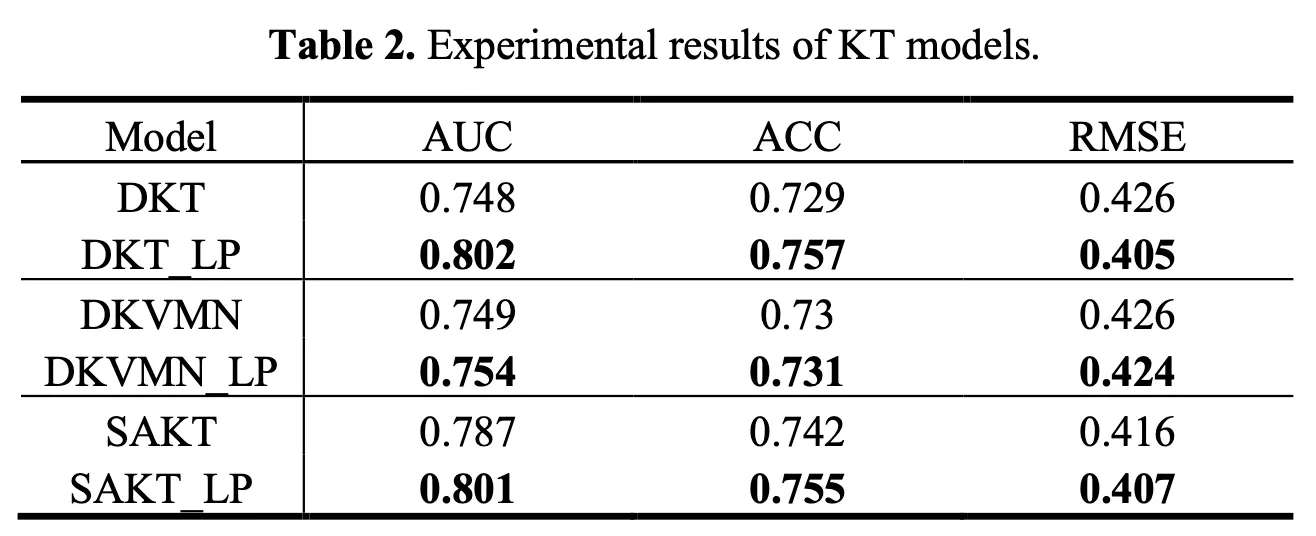
Table 2 displays the experimental results for baseline models with LP information. Model performance was evaluated using the area under the ROC curve (AUC), accuracy (ACC), and root mean square error (RMSE). In the experiment, incorporating LP as side information improved the performance of all metrics across all baseline models. The AUC increased from a minimum of 0.7% to a maximum of 7.2% when LP information was included, ACC increased from a minimum of 0.59% to a maximum of 3.78%, and RMSE decreased by a minimum of 0.31% to a maximum of 4.82%.
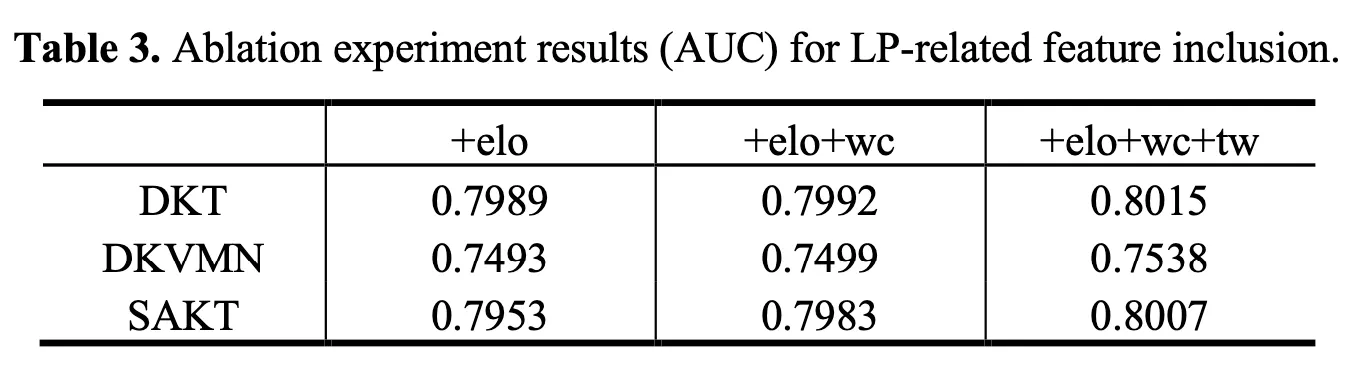
To determine the effect of including features on LP information (Elo rating score, time window feature, and word count), an ablation experiment for each feature was performed. Table 3 lists the results of the ablation experiments where ‘eloelo’ means Elo rating score; ‘wcwc’ means word count of math problems; and ‘twtw’ refers to time windows. The results show that the predictive performance of the model improved when information on LP was incrementally added to each baseline model.

Results of cold start experiment (RQ3)

Similar to many other tasks in machine learning, the KT task has a cold start problem. Cold start problems can be classified into two scenarios [40,44]. The first scenario is a case of constructing a KT model with a small number of students, while the second scenario is a case of constructing a KT model with a short learning activity. We examined whether the LP information could alleviate the cold start issue in these two scenarios. In the first scenario, the performance was compared by reducing the number of training users from 10% to 0.1%. In the second scenario, performance was compared by reducing the sequence length of the training data from 50 to 5.
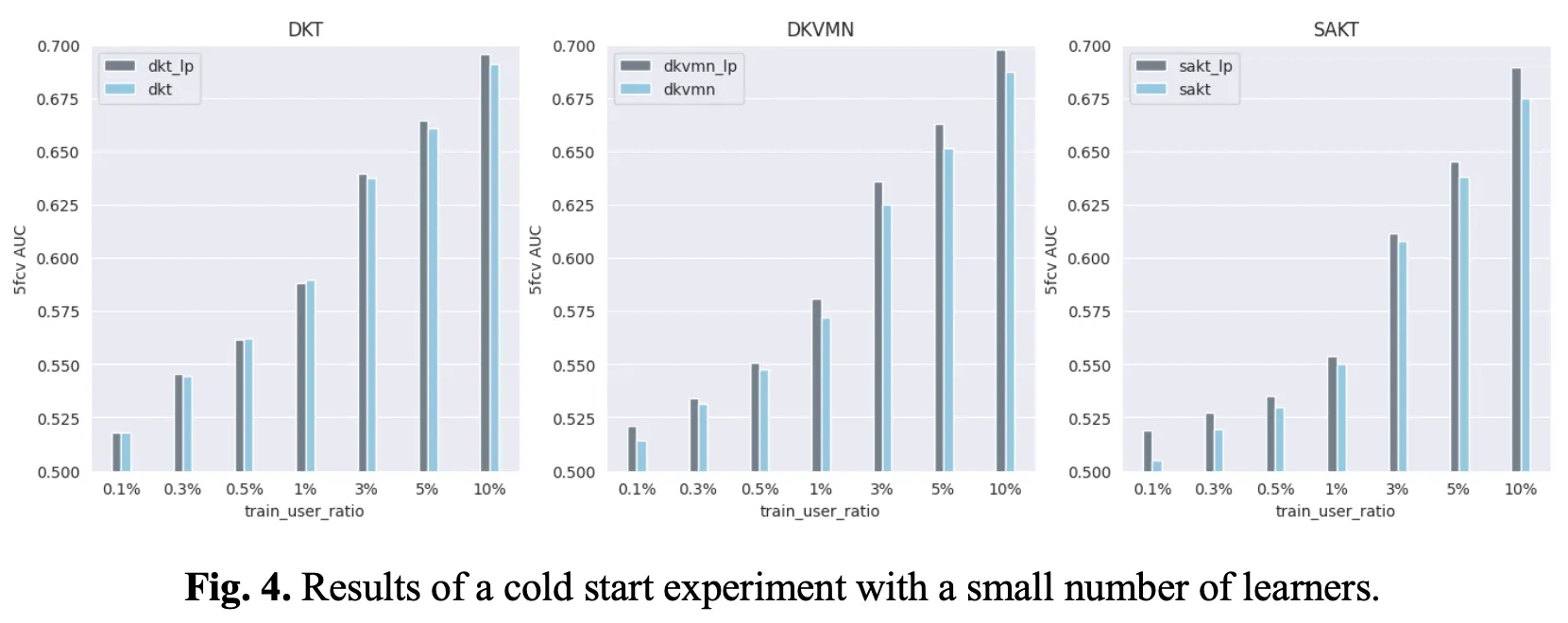
Fig.4 depicts the results of the cold start experiment conducted with a small number of learners (Scenario 1). As a result of the experiment in which the number of training users was reduced from 10% to 0.1%, the model that utilized LP information outperformed the baseline model. Specifically, performance improved by up to 2.12% when only 10% of the train set was used, 1.47% when 1% was used, and 2.76% when 0.1% was used. 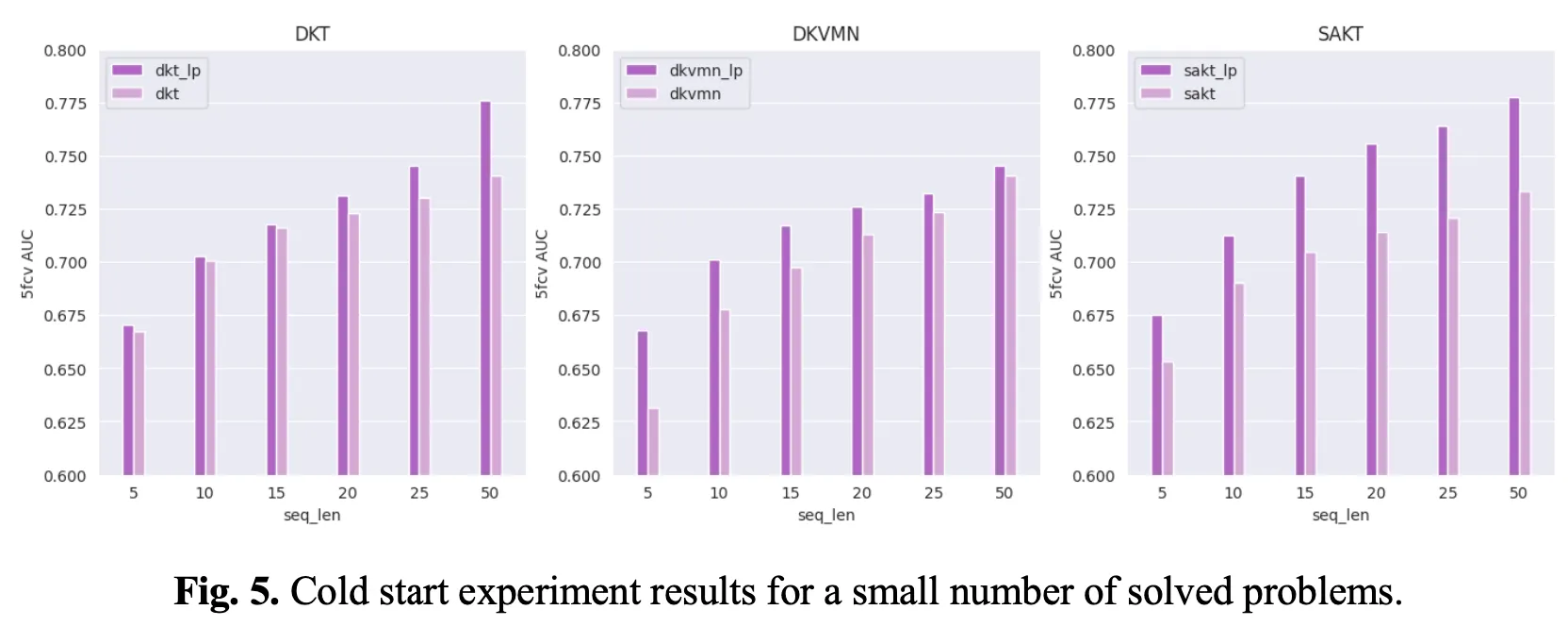On the other hand, Fig.5 depicts the results of a cold start experiment conducted with a small number solved problems (Scenario 2). Experiments with sequence lengths reduced from 50 to 5 revealed that models using LP information outperformed baseline models. Specifically, when using LP information, performance improved by up to 5.74% when 5 problem solving histories were used. Using less than 10 improved performance by up to 3.49%, and using fewer than 15 improved performance by up to 5.08%. In summary, the experiments demonstrate that the AUC performance improved in both scenarios when LP information was included to the three baseline models.

Discussion

Effectiveness of LP information on KT task

Pearson correlation analysis revealed a strong correlation between the sentence length of the math problem and students’ LP. This finding is consistent with previous research showing that LP influences word problem performance in math [12,37]. To the best of our knowledge however, it has yet to be determined whether LP information can be useful side information in a KT task. As a result of the experiment in this study, the performance of all RNN-based, MANN-based, and attention mechanisim-based KT models was enhanced when LP information was utilized. In addition, the ablation study revealed that all three indicators for measuring LP significantly contributed to performance enhancement. This confirms that the learner’s LP information can be meaningfully utilized in the KT task. Furthermore, experiments were carried out to determine whether the learner’s LP information effectively mitigates the cold start problem in the KT field. The experiment confirmed that utilizing LP information to both the scenario of a small number of students and the scenario of a small number of problem-solving alleviated the cold start problem. In summary, using learners’ LP information can improve the performance of KT models, and this information is effective in mitigating the cold start problem.

Possibility as an assistant for educational interventions

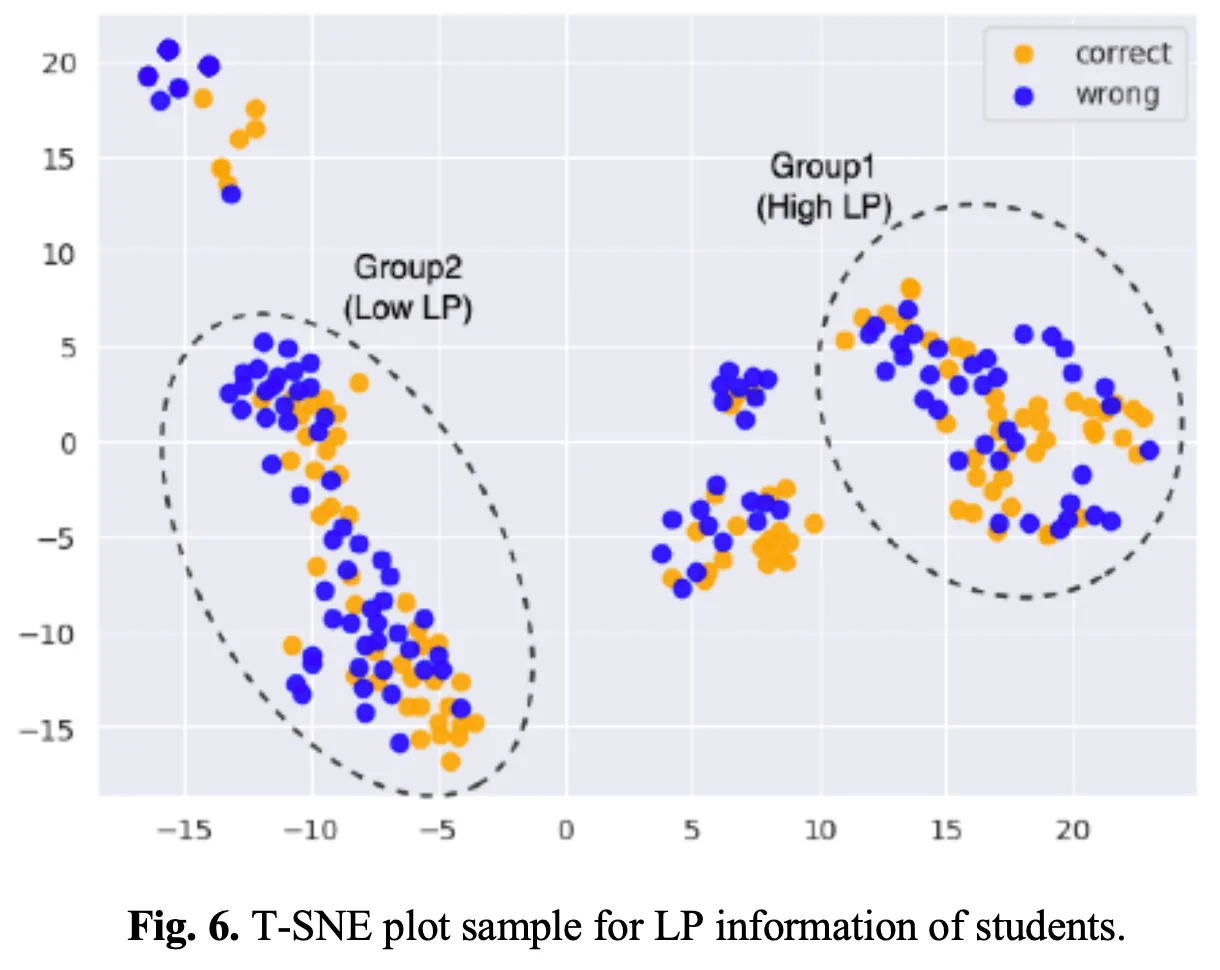
Modeling the learner’s state of knowledge in light of LP has potential as a supplement for educational interventions. Fig.6 depicts the visualization of LP information from students who solved a random word problem using a T-SNE plot [25]. The students’ LP information was encoded using a trained LP-enhanced KT model. Correct responses are marked in orange, while incorrect responses are marked in blue.
In Group 1, students with high LP (high Elo score) were distributed. In the case of students who got the problem wrong in this group, it can be determined that the reason was not because of a lack of LP but because of failure to master the concept related to the problem. As a result, the students in this group who got the problem wrong required educational intervention to master related concepts. Students with low LP (low Elo score) were assigned to Group 2. Students in this group who got the problem wrong, it is likely that they did not comprehend the meaning of the sentence in the problem. As a result, students in this group who were incorrect, required additional educational materials to increase LP as well as additional education on related concepts.

Conclusion

Language proficiency (LP) is a significant factor influencing students’ academic performance. In this study, an LP-enhanced KT model was proposed. The Elo rating scores calculated from the students’ Korean problem-solving data and the number of words in the problem were used as LP information. Furthermore, time window features were used to reflect the updating time of the LP information. Data collected from a real-world online learning platform were used for experiments and data analysis. The analysis revealed a strong correlation between the length of math problems and the average LP of the students who correctly answered the questions. The experiments demonstrated that the LP-enhanced KT model proposed in this study outperformed the other baseline models. Furthermore, when the LP information was incorporated, the cold start problem was alleviated in several scenarios. In future work, the performance of the LP-enhanced knowledge tracing model can be validated for various subjects. Furthermore, additional indicators that can measure students’ LP can be investigated and applied to KT.

References

1.
Abdelrahman, G., Wang, Q.: Knowledge tracing with sequential key-value memory networks. In: Proceedings of the 42nd international ACM SIGIR conference on research and development in information retrieval. pp. 175–184 (2019)
2.
Abdelrahman, G., Wang, Q., Nunes, B.P.: Knowledge tracing: A survey. ACM Computing Surveys (2022)
3.
Adegboye, A.: Proficiency in english language as a factor contributing to competency in mathematics. Education today 6(2), 9–13 (1993)
4.
Aina, J.K., Ogundele, A.G., Olanipekun, S.S.: Students’ proficiency in english language relationship with academic performance in science and technical education. American Journal of Educational Research 1(9), 355–358 (2013)
5.
Barkaoui, K.: Examining repeaters’ performance on second language proficiency tests: A review and a call for research. Language Assessment Quarterly 14(4), 420–431 (2017)
6.
Bastug, M.: The structural relationship of reading attitude, reading comprehension and academic achievement. International Journal of Social Sciences and Education 4(4), 931–946 (2014)
7.
Batchelder, W.H., Bershad, N.J.: The statistical analysis of a thurstonian model for rating chess players. Journal of Mathematical Psychology 19(1), 39–60 (1979)
8.
Chan, W.L., Yeung, D.Y.: Clickstream knowledge tracing: Modeling how students answer interactive online questions. In: LAK21: 11th International Learning Analytics and Knowledge Conference. pp. 99–109 (2021)
9.
Chen, P., Lu, Y., Zheng, V.W., Pian, Y.: Prerequisite-driven deep knowledge tracing. In: 2018 IEEE International Conference on Data Mining (ICDM). pp. 39–48. IEEE (2018)
10.
Choffin, B., Popineau, F., Bourda, Y., Vie, J.J.: Das3h: modeling student learning and forgetting for optimally scheduling distributed practice of skills. arXiv preprint arXiv:1905.06873 (2019)
11.
Elo, A.E.: The rating of chessplayers, past and present. Arco Pub. (1978)
12.
Fuchs, L.S., Fuchs, D., Compton, D.L., Hamlett, C.L., Wang, A.Y.: Is word-problem solving a form of text comprehension? Scientific Studies of Reading 19(3), 204–223 (2015)
13.
Ghosh, A., Heffernan, N., Lan, A.S.: Context-aware attentive knowledge tracing. In: Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining. pp. 2330–2339 (2020)
14.
Hochreiter, S., Schmidhuber, J.: Long short-term memory. Neural computation 9(8), 1735–1780 (1997)
15.
Izatullah, S., Nasir, R., Gul, F.: A study to examine the relationship between english language proficiency and academic achievement of students in higher education institutions. Global Educational Studies Review, VII (2022)
16.
Jun, W.: A study on correlation analysis of academic performance per subject for the gifted children in IT. Journal of Gifted/Talented Education 23(3), 407–419 (2013)
17.
Kim, S., Kim, W., Jung, H., Kim, H.: Dikt: Dichotomous knowledge tracing. In: Intelligent Tutoring Systems: 17th International Conference, ITS 2021, Virtual Event, June 7–11, 2021, Proceedings 17. pp. 41–51. Springer (2021)
18.
Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014)
19.
Lee, W., Chun, J., Lee, Y., Park, K., Park, S.: Contrastive learning for knowledge tracing. In: Proceedings of the ACM Web Conference 2022. pp. 2330–2338 (2022)
20.
Lindsey, R.V., Shroyer, J.D., Pashler, H., Mozer, M.C.: Improving students’ long-term knowledge retention through personalized review. Psychological science 25(3), 639–647 (2014)
21.
Liu, Q., Huang, Z., Yin, Y., Chen, E., Xiong, H., Su, Y., Hu, G.: Ekt: Exercise-aware knowledge tracing for student performance prediction. IEEE Transactions on Knowledge and Data Engineering 33(1), 100–115 (2019)
22.
Liu, Q., Shen, S., Huang, Z., Chen, E., Zheng, Y.: A survey of knowledge tracing. arXiv preprint arXiv:2105.15106 (2021)
23.
Liu, Y., Yang, Y., Chen, X., Shen, J., Zhang, H., Yu, Y.: Improving knowledge tracing via pre-training question embeddings. arXiv preprint arXiv:2012.05031 (2020)
24.
Liu, Z., Liu, Q., Chen, J., Huang, S., Tang, J., Luo, W.: pykt: A python library to benchmark deep learning based knowledge tracing models. arXiv preprint arXiv:2206.11460 (2022)
25.
Van der Maaten, L., Hinton, G.: Visualizing data using t-sne. Journal of machine learning research 9(11) (2008)
26.
Nakagawa, H., Iwasawa, Y., Matsuo, Y.: Graph-based knowledge tracing: modeling student proficiency using graph neural network. In: IEEE/WIC/ACM International Conference on Web Intelligence. pp. 156–163 (2019)
27.
Pandey, S., Karypis, G.: A self-attentive model for knowledge tracing. arXiv preprint arXiv:1907.06837 (2019)
28.
Pela ́nek, R.: Applications of the elo rating system in adaptive educational systems. Computers & Education 98, 169–179 (2016)
29.
Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L.J., Sohl-Dickstein, J.: Deep knowledge tracing. Advances in neural information processing systems 28 (2015)
30.
Racca, R., Lasaten, R.C.S.: English language proficiency and academic performance of philippine science high school students. International Journal of Languages, Literature and Linguistics 2(2), 44–49 (2016)
31.
Shen, S., Liu, Q., Chen, E., Huang, Z., Huang, W., Yin, Y., Su, Y., Wang, S.: Learning process-consistent knowledge tracing. In: Proceedings of the 27th ACM SIGKDD conference on knowledge discovery & data mining. pp. 1452–1460 (2021)
32.
Shen, S., Liu, Q., Chen, E., Wu, H., Huang, Z., Zhao, W., Su, Y., Ma, H., Wang, S.: Convolutional knowledge tracing: Modeling individualization in student learning process. In: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. pp. 1857–1860 (2020)
33.
Shin, D., Shim, Y., Yu, H., Lee, S., Kim, B., Choi, Y.: Saint+: Integrating temporal features for ednet correctness prediction. In: LAK21: 11th International Learning Analytics and Knowledge Conference. pp. 490–496 (2021)
34.
Song, X., Li, J., Lei, Q., Zhao, W., Chen, Y., Mian, A.: Bi-clkt: Bi-graph contrastive learning based knowledge tracing. Knowledge-Based Systems 241, 108274 (2022)
35.
Stoffelsma, L., Spooren, W.: The relationship between english reading proficiency and academic achievement of first-year science and mathematics students in a multilingual context. International Journal of Science and Mathematics Education 17, 905–922 (2019)
36.
Su, Y., Liu, Q., Liu, Q., Huang, Z., Yin, Y., Chen, E., Ding, C., Wei, S., Hu, G.: Exercise-enhanced sequential modeling for student performance prediction. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 32 (2018)
37.
Vilenius-Tuohimaa, P.M., Aunola, K., Nurmi, J.E.: The association between mathematical word problems and reading comprehension. Educational Psychology 28(4), 409–426 (2008)
38.
Virtanen, P., Gommers, R., Oliphant, T.E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S.J., Brett, M., Wilson, J., Millman, K.J., Mayorov, N., Nelson, A.R.J., Jones, E., Kern, R., Larson, E., Carey, C.J., Polat, I ̇., Feng, Y., Moore, E.W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E.A., Harris, C.R., Archibald, A.M., Ribeiro, A.H., Pedregosa, F., van Mulbregt, P., SciPy 1.0 Contributors: SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods 17, 261–272 (2020). https://doi.org/10.1038/s41592-019-0686-2
39.
Wang, J.: Relationship between mathematics and science achievement at the 8th grade. Online Submission 5, 1–17 (2005)
40.
Wu, Z., Huang, L., Huang, Q., Huang, C., Tang, Y.: Sgkt: Session graph-based knowledge tracing for student performance prediction. Expert Systems with Applications 206, 117681 (2022)
41.
Yang, Y., Shen, J., Qu, Y., Liu, Y., Wang, K., Zhu, Y., Zhang, W., Yu, Y.: Gikt: a graph-based interaction model for knowledge tracing. In: Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2020, Ghent, Belgium, September 14–18, 2020, Proceedings, Part I. pp. 299–315. Springer (2021)
42.
Zhang, J., Shi, X., King, I., Yeung, D.Y.: Dynamic key-value memory networks for knowledge tracing. In: Proceedings of the 26th international conference on World Wide Web. pp. 765–774 (2017)
43.
Zhang, M., Zhu, X., Zhang, C., Ji, Y., Pan, F., Yin, C.: Multi-factors aware dual-attentional knowledge tracing. In: Proceedings of the 30th ACM International Conference on Information & Knowledge Management. pp. 2588–2597 (2021)
44.
Zhao, J., Bhatt, S., Thille, C., Gattani, N., Zimmaro, D.: Cold start knowledge tracing with attentive neural turing machine. In: Proceedings of the Seventh ACM Conference on Learning@ Scale. pp. 333–336 (2020)
저자 정희석 (Heeseok Jung) 고려대학교에서 컴퓨터학 전공으로 학,석사학위를 취득 후, 현재 클래스팅 AI Researcher로 재직중이다. 추천 시스템, 지식 추적 등과 같은 AIed에 관심을 가지고 연구하고 있다. poco2889@classting.com